Karplus, Strong und die Saite (1)
Kevin Karplus und Alex Strong stellten 1983 im Computer Music Journal einen Algorithmus vor, mit dem sich Saiteninstrumente imitieren lassen. Das frappierende daran ist das Ausgangsmaterial: Ein Rauschen!
[01]
Um was wird es gehen?
Der ‚Karplus-Strong-Algorithmus‘, der 1987 patentiert wurde, hört sich auf den ersten Blick etwas kompliziert an, lässt sich aber mit Reaktor recht leicht nachbauen. Die Idee ist folgende: Ein Speicher wird mit einer bestimmten Anzahl Samples gefüllt. Danach verlassen die Samples der Reihe nach den Speicher, durchlaufen einen Filter (in dem sie modifiziert werden) und landen anschließend wieder im Speicher um den Kreislauf von vorne zu beginnen. Da das alles sehr schnell passiert, entsteht ein psychoakustisches Phänomen, „Periodicity Pitch“ genannt. Die hierbei wahrgenommene Tonhöhe entspricht der Anzahl der Samples pro Sekunde im Kreislauf, geteilt durch der Anzahl der insgesamt verwendeten Samples.
Wer tiefer in die Mathematik dahinter einsteigen möchte, wird auf der Website der Standford University fündig.
Das Grundkonstrukt werden wir sehr viel einfacher halten, auch wenn die Anzahl der Module ziemlich schnell anwachsen wird. Aber das sind zum großen Teil immer wiederkehrende Elemente, die wir am Ende – ihr kennt das schon – sauber in diversen Macros unterbringen.
Das Tutorial ist etwas umfangreicher und deshalb zweiteilig angelegt:
- Teil 1 – Die Saite als solches
- Rausch-Oszillator und Oszilloskop erstellen
- Rauschen mit einer Hold-Envelope auf einen tonhöhenabhängigen Implus begrenzen
- Synthese-Kreislauf erstellen
- Spaß mit der Tonhöhenkonstante
- Teil 2 – Optimierungen für ein natürliches Verhalten
- Hold-Evelope durch AD-Evelope ersetzen und an die Tonhöhe koppeln
- Alle relevanten ‚Stellschrauben‘ modulierbar machen (zufällige Variationen des Saitenverhaltens)
- Filterbank ergänzen
- Klangregelung und Ausgang erstellen
Am Ende der beiden Teile werdet ihr das komplette Projekt für euren Reaktor herunteladen können.
Wichtig: Ich habe das Konstrukt von vornherein 8-stimmig polyphon angelegt. Wie das geht, ist hier erklärt.
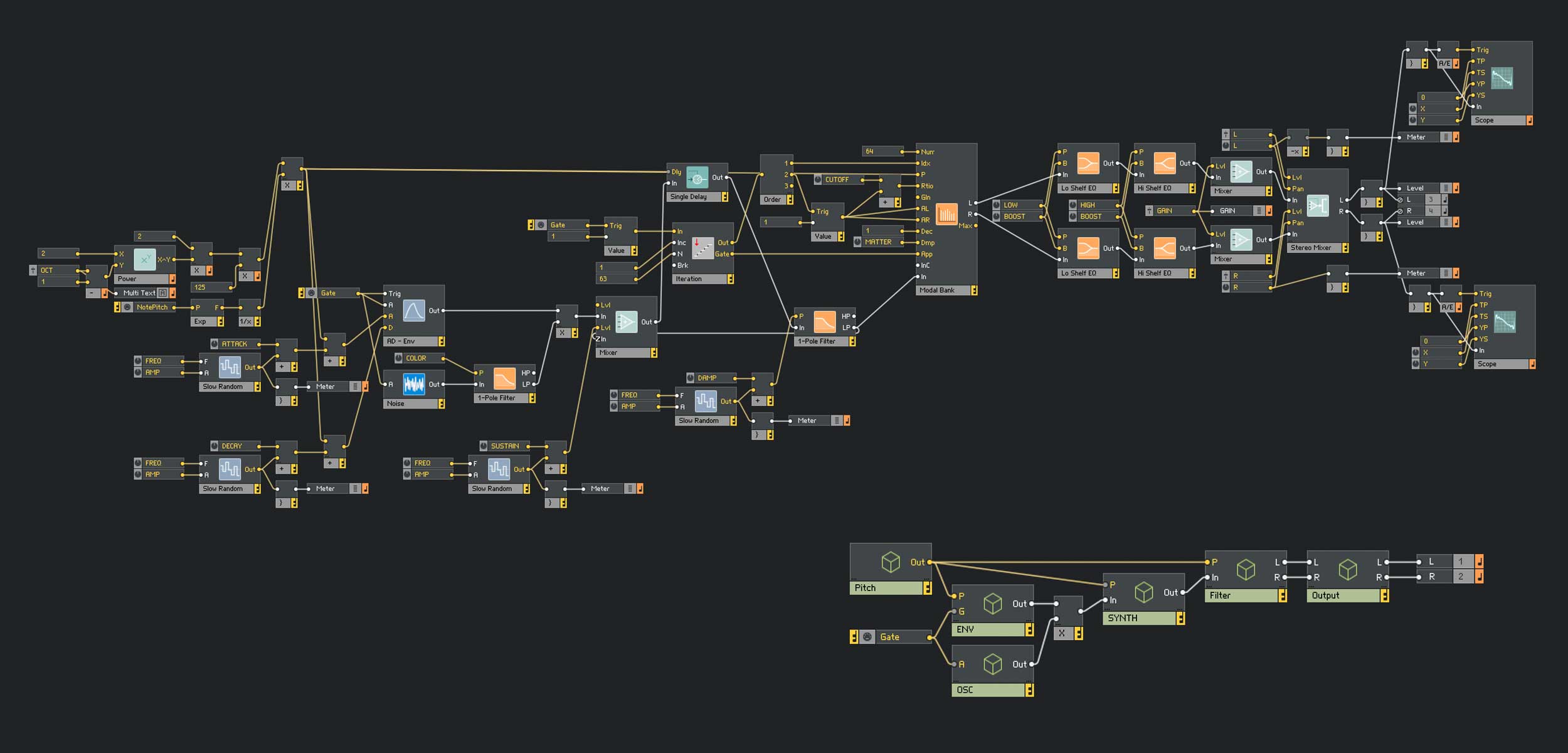
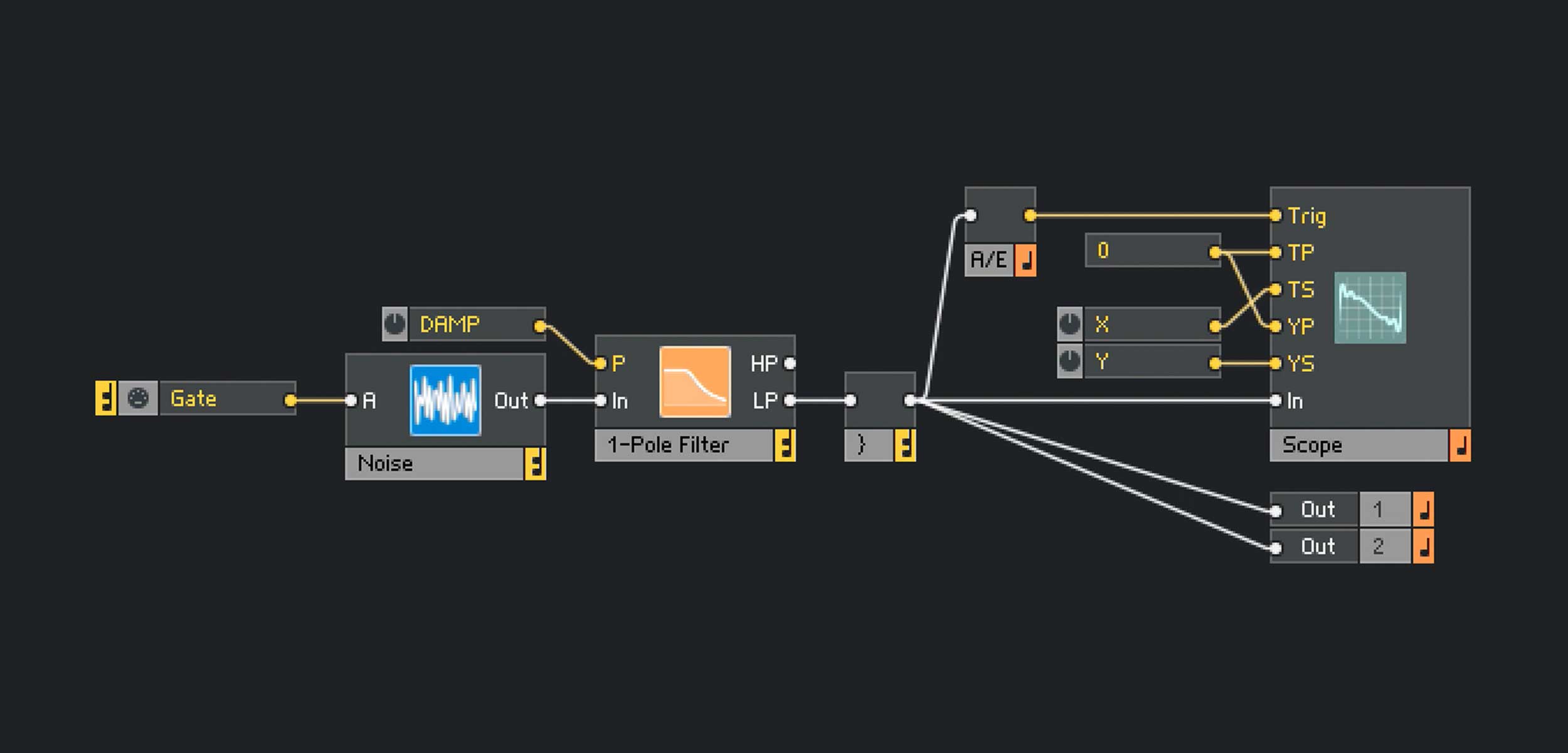
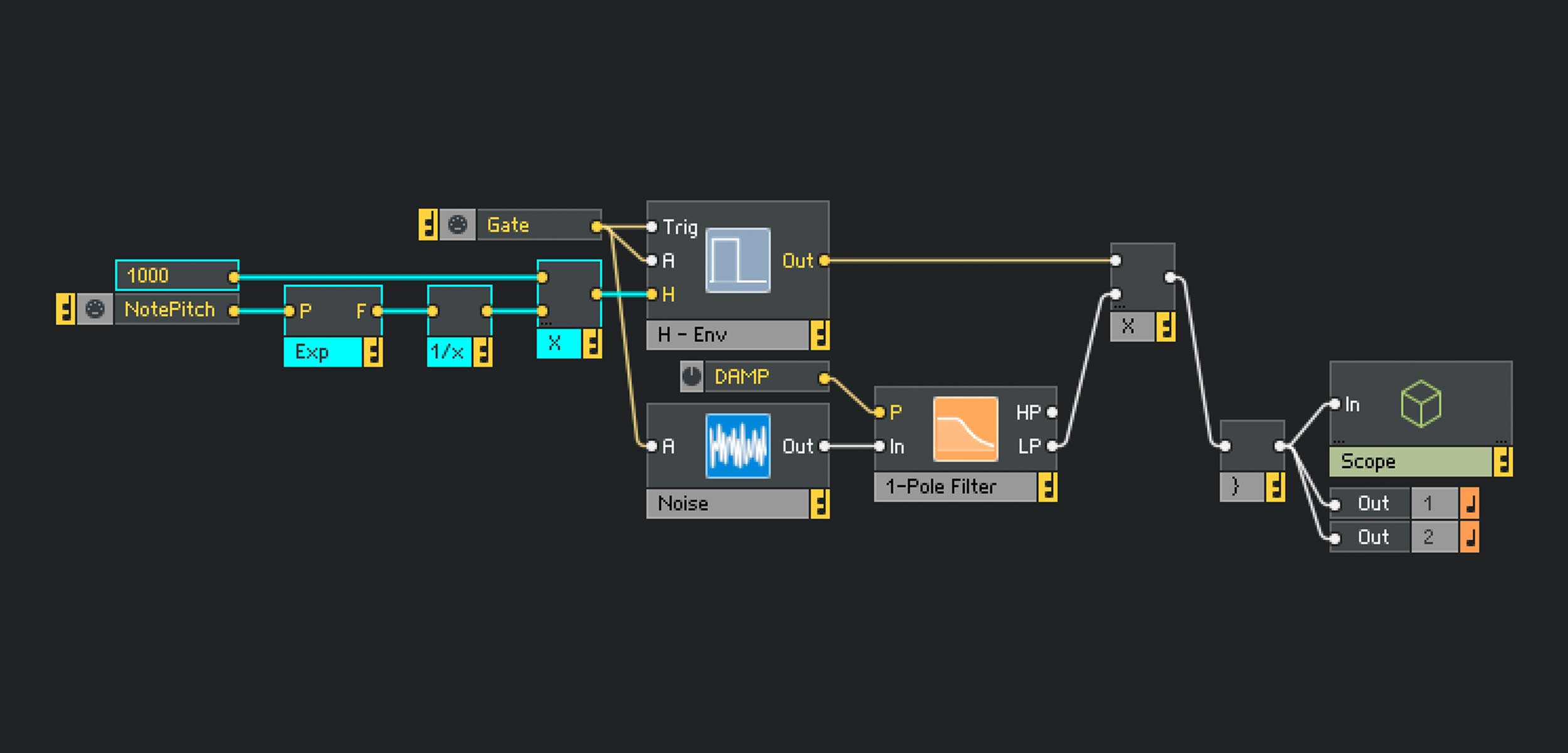
Abb. 1: Die Anatomie der Saitenschaltung
[02]
Rauschgenerator und Oszilloskop
Für unseren Saitengenerator werden wie keine Rausch-Samples in Speicher füllen, sondern statt dessen einen banalen Rausch-Oszillator bemühen. Diesem werden wir im nächsten Schritt beibringen, kurze Impulse zu erzeugen. Damit ist der Vorgabe Genüge getan.
Für das Rauschen genügen Das Gate-Modul und der Rausch-Oszillator selbst. Der nachgeschaltete Pole-Filter erlaubt das regeln hoher Frequenzen (Damp), was den Saitenklang später etwas weicher und angenehmer erscheinen lässt:
- Kontextmenü > Build-In- Modules > MIDI In > Gate
- Kontextmenü > Build-In- Modules > Oscillator > Noise
- Kontextmenü > Build-In- Modules > Panel > Knob
- Damp > Min: 20, Max: 120, Step Size 0, nach eigenem Bedürfnis.
- Kontextmenü > Build-In- Modules > Filter > HP/LP 1-Pole
- Kontextmenü > Build-In- Modules > Auxiliary > Audio Voice Combiner.
der Audio-Voice-Combiner hinter dem Filter sorgt dafür, dass alle monophonen Elemente (wie z B,. das Scope-Modul und die Reaktor-Ausgänge, die grundsätzlich nur monophon ausgelegt sind), mit der polyphonen Ausgabe klarkommen.
Das Oszilloskop bauen wir uns wieder mit einem Scope-Modul, verzichten aber auf die aufwändige Y-Skalierung aus dem Tutorial-Synthesizer, weil uns hier nicht so viele Überraschungen erwarten.
Die Scope-Eingänge TP und YP (Time-Position, Y-Position) setzen wir mit einer Konstanten auf 0 (vertikal links und horizontal mittig), das Triggersignal entnehmen wir dem Audiosignal (via mono-geschaltetem(!) Audio-To-Event-Converter). Die Eingänge TS und YS (Time-Scale, Y-Scale) erhalten jeweils einen Drehregler zum skalieren der Anzeige. Das war es auch schon:
- Kontextmenü > Build-In- Modules > Auxillary > A to E
- Kontextmenü > Build-In- Modules > Math > Constant
- Kontextmenü > Build-In- Modules > Panel > Knob
- X > Min: 1, Max: 10, Step Size: 0, Default: nach eigenem Bedürfnis.
- Y > Min: 0.1, Max: 4, Step Size: 0, Default: nach eigenem Bedürfnis.
- Kontextmenü > Build-In- Modules > Panel > Scope
Soweit dürfte die Schaltung keine Rätsel aufgeben.
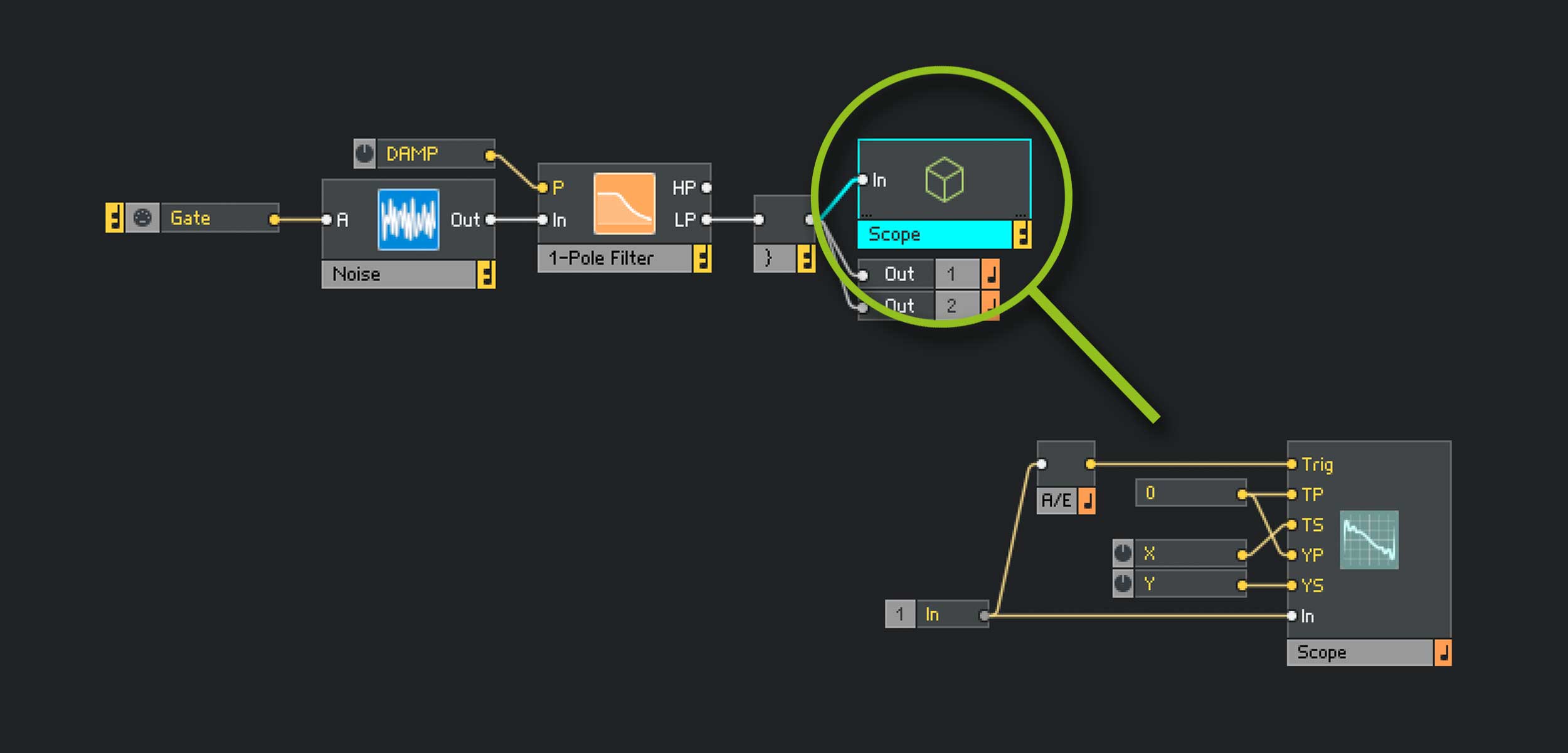
Abb. 2: Rausch-Oszillator und Oszilloskop
Abb. 3: GUI – Serviervorschlag
Rausch-Oszillator
So hört sich unsere „Saite“ fürs Erste an. Ein banales Rauschen mit einer Filteroption und jeder Menge Obertönen mit ständig wechselnder Frequenz. Das ist wichtig!
Bevor es weiter geht …
packen wir unser Oszilloskop in ein Macro, um schon mal etwas Übersicht zu schaffen:
[03]
Tonhöhenabhängigen Rauschimpuls erzeugen
Um das Rauschen zu einem Impuls zu verkürzen, bedienen wir uns zunächst einmal einer Hold-Envelope. Diese rudimentäre Hüllkurve verfügt lediglich über eine Hold-Time, die festlegt, wie lange das Signal einen maximalen Pegel aufweist. Danach fällt das Signal sofort auf 0. Das Geschehen ist so einfacher nachzuvollziehen, als mit der AD-Hüllkurve, die wir später an dieser Stelle verwendenden werden:
- Kontextmenü > Build-In- Modules > MIDI In > Note Pitch
- Kontextmenü > Build-In- Modules > LFO, Envelope > H
- Kontextmenü > Build-In- Modules > Math > Multiply
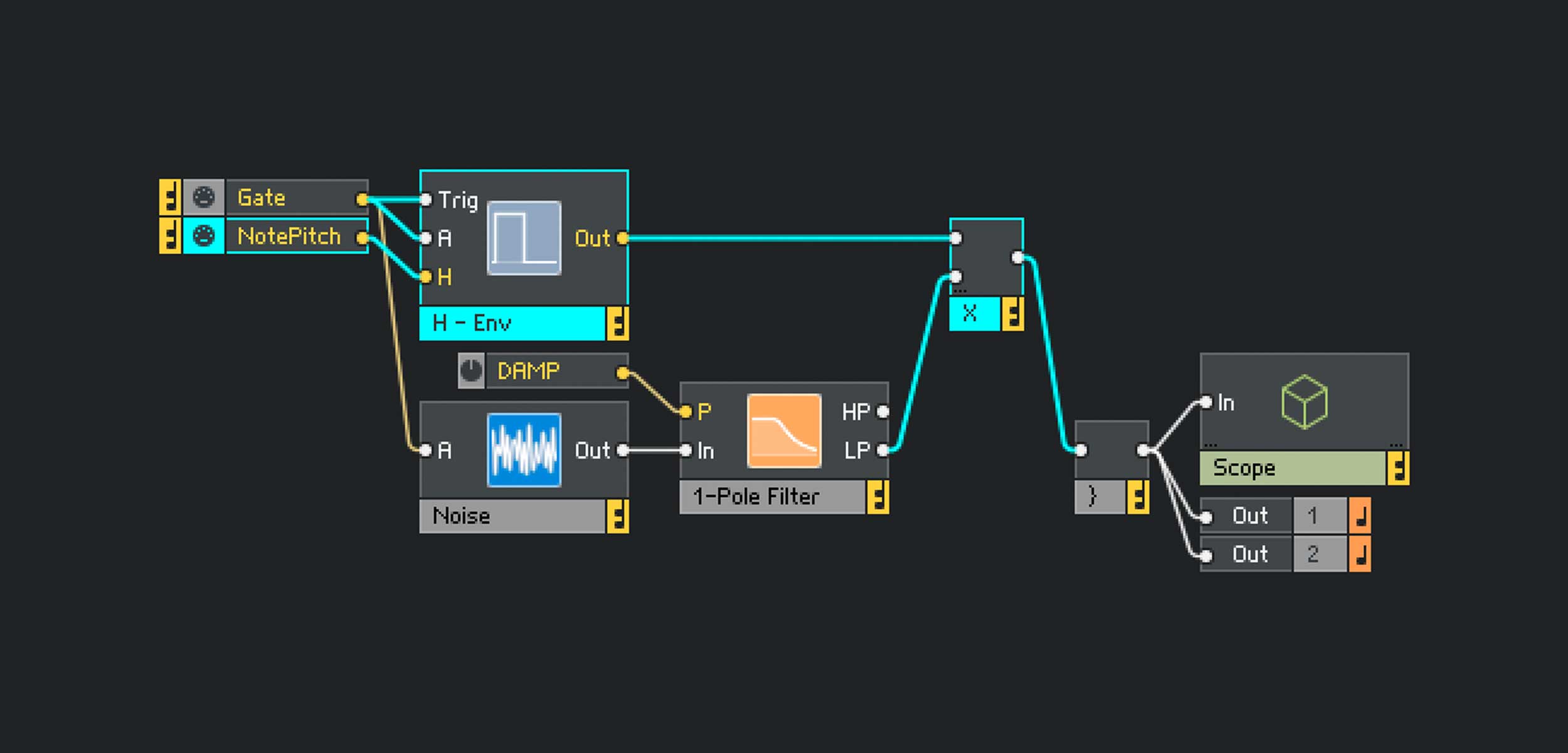
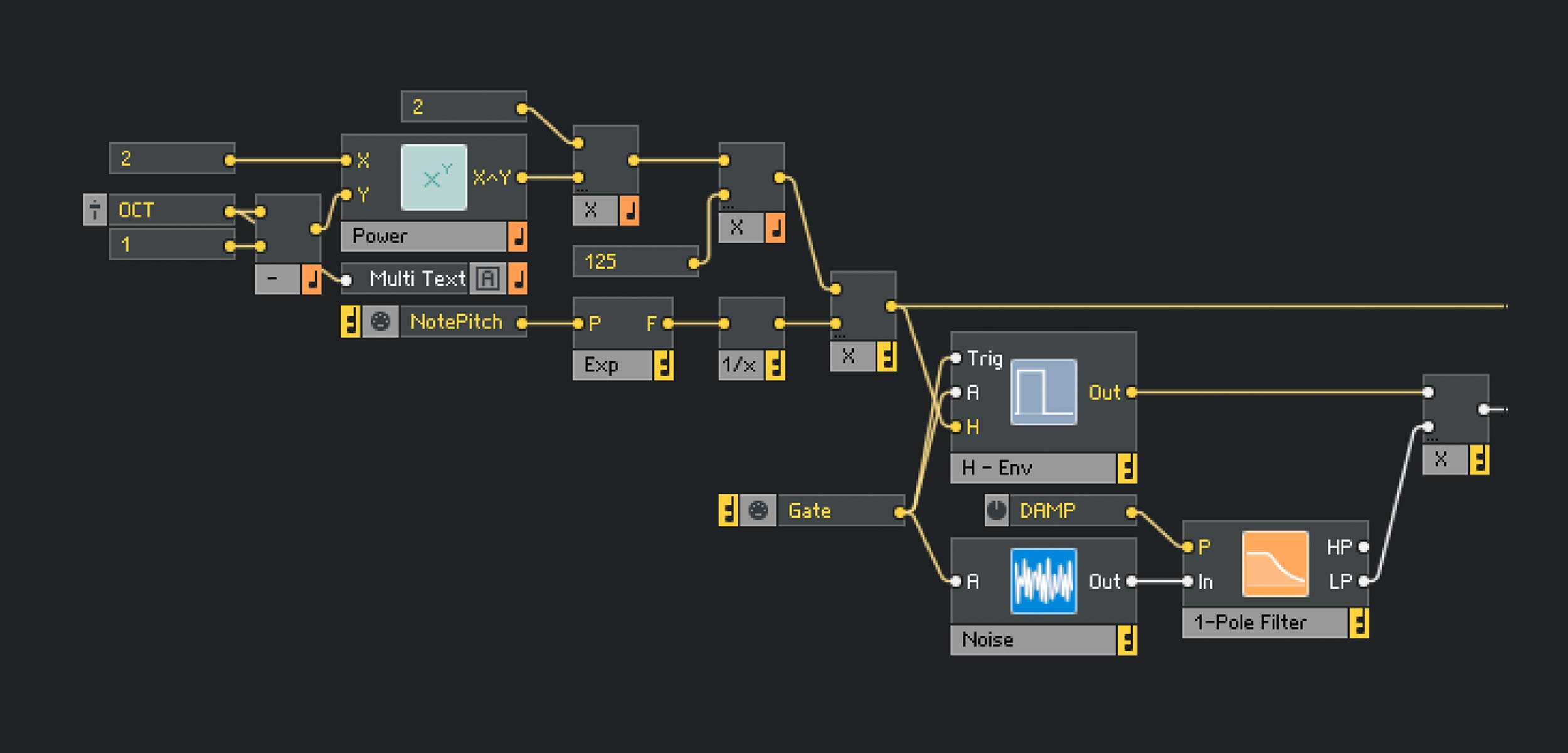
Das Gate-Modul bedient nun ausser dem A-Eingang des Rausch-Oszillators noch die Eingänge Trig und A der Hold-Envelope. Das NotePitch-Modul versorgt den H-Eingang der Hold-Envelope, womit die Signaldauer an die Tonhöhe gekoppelt ist. Der Hüllkurven-Ausgang und der Filter-Ausgang des des Oszillators werden über einen Multiplikator zusammengeführt. Das Ergebnis ist das selbe, wie wenn wir den Hüllkurven-Ausgang an den A-Eingang des Rausch-Oszillators angeschlossen hätten. Mit dieser Verschaltung bleibt der Eingang des Oszillators aber für weitere Manipulationen besser zugänglich.
Wenn ihr das Ergebnis ausprobiert, werdet ihr feststellen, dass sich die Dauer des Rauschens tatsächlich an die Tonhöhe anpasst. allerdings nicht ganz wie erwünscht. Was wir bräuchten, wäre eine Signaldauer, die mit zunehmender Tonhöhe kürzer wird (hohe Töne verklingen schneller, als tiefe) – und deutlich kürzere Impulse! Was wir im Moment hören, ist in allen Bereichen das genaue Gegenteil…
Abb. 5: H-Envelope
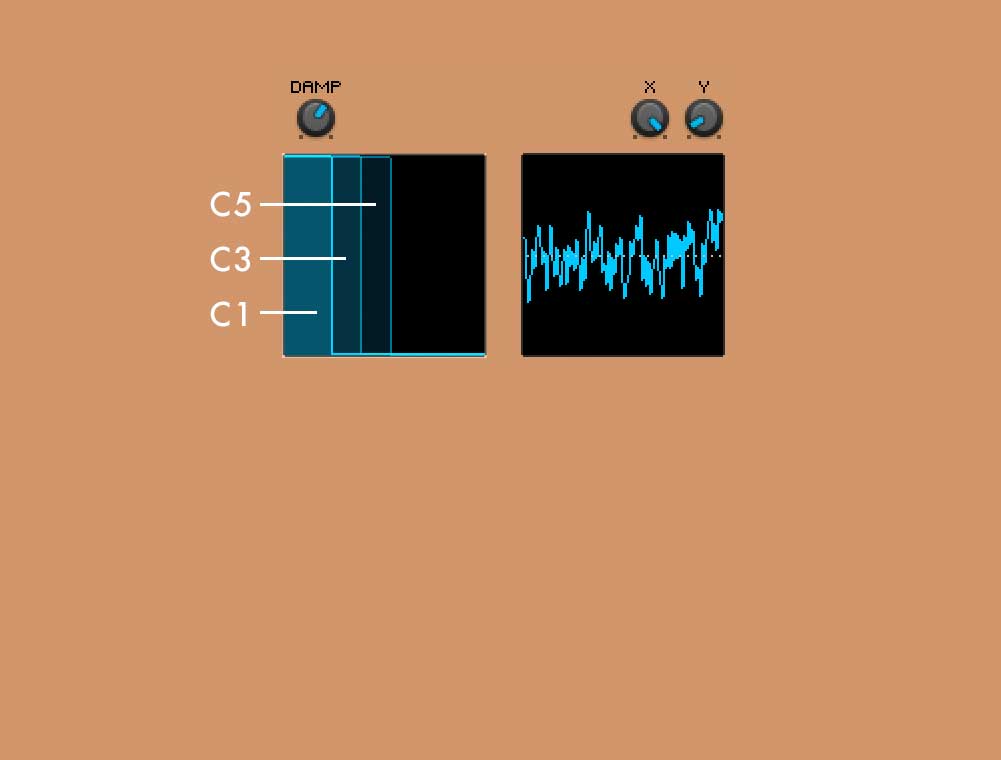
Abb. 6: GUI – Serviervorschlag
H-Envelope: C1 - C4
Das Verhalten der H-Envelope bei den Noten C1, C2, C3 und C4. Ihr erkennt die extreme Zunahme der Dauer. Das C5 aus der Grafik habe ich uns hier erspart. Es dauert satte 16 Sekunden – Ein wenig zu lang für unsere Zwecke …
Um dieses Problem zu lösen, müssen wir ein wenig Mathematik betreiben:
- Kontextmenü > Build-In- Modules > Math > Constant
- Kontextmenü > Build-In- Modules > Math > Expon. (F)
- Kontextmenü > Build-In- Modules > Math > 1/x
- Kontextmenü > Build-In- Modules > Math > Multiply
Der NotePitch-Wert durchläuft erst das Exponent (F)-Modul, das aus den Halbtonschritten die passende Frequenz in Hz erzeugt. Mit dem nachfolgenden 1/x-Modul erhalten wir die resultierende Signaldauer in Millisekunden. Jetzt müssen wir das Ergebnis nur noch mit 1000 multiplizieren, um auf die korrekte Tonhöhe zu kommen.
Letzteres ist eine Behauptung, die ihr einfach glauben müsst, weil wir dem Rausch-Impuls noch keine Tonhöhe entnehmen können. Dazu muss erst der Synthese-Kreislauf komplett sein. Bei der Gelegenheit: Mit der Konstanten 1000 werden wir uns am Ende des 1. Teils noch einen kleinen mathematischen Spaß erlauben. Laßt euch überraschen.
Abb. 7: Korrigierte Hold-Time
Abb. 8: GUI – Serviervorschlag
H-Envelope: C1 - C5, Impuls
Jetzt haben die Impulse die richtige Länge. In jedem Impuls steckt das komplette Spektrum des Rauschens – und das ist alles, was wir für die Saite benötigen. An dieser Stelle habt ihr zum letzten Mal ein Rauschen gehört.
[04]
Jetzt kommt der Augenblick …
in dem wir den Rausch-Impuls in eine Saite verwandeln. It’s Magic! Alles, was wir dazu brauchen, sind 4 verschiedene Modul-Typen in veränderlichen Mengen:
- Kontextmenü > Build-In- Modules > Signal Path > Amp/Mixer (2)
- Kontextmenü > Build-In- Modules > Delay > Single Delay
- Kontextmenü > Build-In- Modules > Filter > HP/LP 1-Pole
- Kontextmenü > Build-In- Modules > Panel > Knob (3)
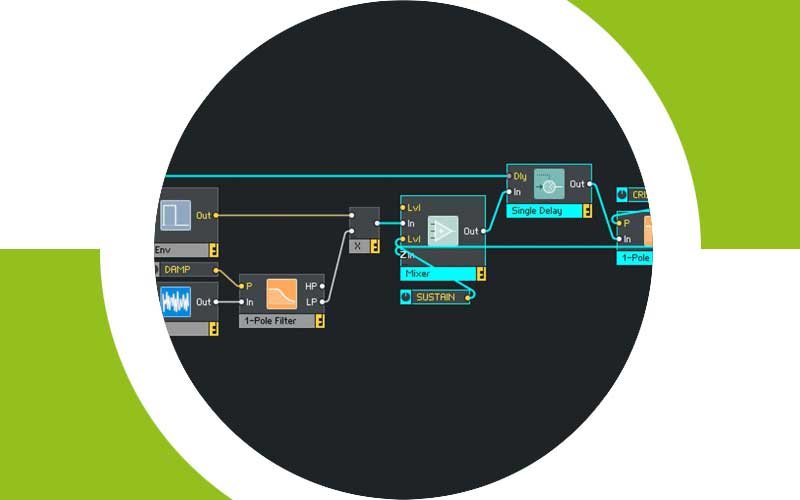
Unser Rausch-Impuls landet, nachdem er den Filter hinter dem Oszillator verlassen hat, im ersten Mixer-Modul und von dort im Single-Delay. Der Dly-Eingang des Single-Delays wird von der selben Note-Pitch-Schaltung bedient, wie der H-Eingang der Hold-Envelope. Anschließend läuft der, um seine eigene Dauer verzögerte Rausch-Impuls durch den 1-Pole-Filter und durch einen zweiten Mixer, mit dem wir die Lautstärke regeln, in den Reaktor-Ausgang.
Noch klingt nichts nach einer Saite, weil der entscheidende Trick noch fehlt: Der Ausgang des 1-Pole-Filters wird nun zum ersten Mixer zurückgeführt und dort in einen weitern Eingang geleitet. Wie ihr beim Mixer (und allen anderen Eingangsseitig erweiterbaren Modulen) weitere Anschlüsse erzeugt, könnt ihr hier nochmal nachschauen.
Damit haben wir ein Feedback erstellt, was uns Reaktor mit einem „Z“ am Mixer-Eingang signalisiert. Und weil das ein Feedback ist, müssen wir mit dem Level sehr behutsam umgehen, weil sich sonst unschönes ereignet. Deshalb gleich weiter zum nächsten Schritt …
Bleiben noch die drei Drehregler, mit denen wir Einfluss auf das Geschehen nehmen wollen/müssen:
- Der erste Knopf regelt den Level des Feedback-Signals: Min: -0.9, Max: -0.05. Step Size: 0, Default nach eigenem Bedürfnis.
- Der zweite Knopf regelt die Filterfrequenz und damit die Helligkeit/Agressivität des Klanges: Min: 60, Max: 180. Step Size: 0, Default nach eigenem Bedürfnis.
- Der dritte und letzte Knopf ist für die Lautstärke zuständig: Min: -0.9, Max: 60. Step Size: 0, Default nach eigenem Bedürfnis.
Und fertig ist unsere rudimentäre Saite.
Abb. 9: Der Synthesekreislauf
Abb. 10: GUI – Serviervorschlag
Die rudimentäre Saite
So klingt unsere erste, aus Rauchen generierte Saite. In den unteren Frequenzen etwas besser, weiter oben noch etwas dünn. Und vor allem bei jedem Anschlag nahezu gleich. Das werden wir aber im zweiten Teil dieses Tutorials beheben.
[05]
Spaß mit Mathe
Wie in Abschnitt [3] angekündigt, folgt nun eine mathematische Einlage.
Wem das zu kompliziert ist, der kann das ignorieren. Dieser Schritt ist optional und für den weiteren Verlauf nicht wichtig. Man kann hier aber prima sehen, wie sich mit Reaktor auch mahematische Formeln umsetzen lassen.
Wie bereits erwähnt, ist die Konstante 1000 in der Note-Pitch-Berechnung für die korrekte Tonhöhe der Saite verantwortlich. Daraus folgt: Andere Werte haben andere Tonhöhen zur Folge. Nun ergibt sicher nicht jeder beliebige Wert einen Sinn. Aber eine Oktavierungsfunktion wäre ganz schick. Die entsprechenden Werte für das Oktavieren sehen woe folgt aus:
+2: 250 / +1: 500 / 0: 1000 / +1: 2000 / +2: 4000
Das Problem liegt auf der Hand: Die Reihenfolge ist nicht linear. Ein Regler/Fader mit Min: 250 und einer fixen Step Size scheidet erst mal aus, da diese sich von Schritt zu Schritt verdoppeln müsste. Eine Vorgabe, die Reaktor nicht erfüllen kann. Alternativ könnte man ein List-Modul anlegen und dort die Werte eintragen. Das hätte aber eine sperrige Darstellung von Text, Menü oder vertikalen Buttons (5 an der Zahl) zur Folge. Weil das hübscher aussieht, soll es ein horizontaler Fader werden – schließlich will ich euch zeigen, wie man in Reaktor Formeln bauen kann 😉
Abb. 11: Die Oktavierungs-Logik
Wie ihr sehen könnt, ist die Konstante 1000 durch 10 weitere Module ersetzt worden, die folgendes leisten:
Aus einem horizontalen Fader, der die Werte 1, 2, 3, 4, und 5 ausgibt, werden am Ende die Werte 250, 500, 1000, 2000 und 5000. Dazu gibt es eine nette kleine Formel, die wir mit ein paar Mathe-Modulen nachbauen. Der Einfachheit halber sind alle Module auf Mono gesetzt, um zusätzliche Audio Voice Combiner zu vermeiden. Unsere Einkaufsliste lautet:
- Kontextmenü > Build-In- Modules > Panel > Fader
- OCT: Min: 5, Max: 1, Step Size 1, Default: 3
- Kontextmenü > Build-In- Modules > Math > Constant (4)
- Kontextmenü > Build-In- Modules > Math > Multiply (2)
- Kontextmenü > Build-In- Modules > Math > Subtract
- Kontextmenü > Build-In- Modules > Math > Power, x^y
- Kontextmenü > Build-In- Modules > Panel > Multitext
Aus der Nähe sieht das dann so aus:
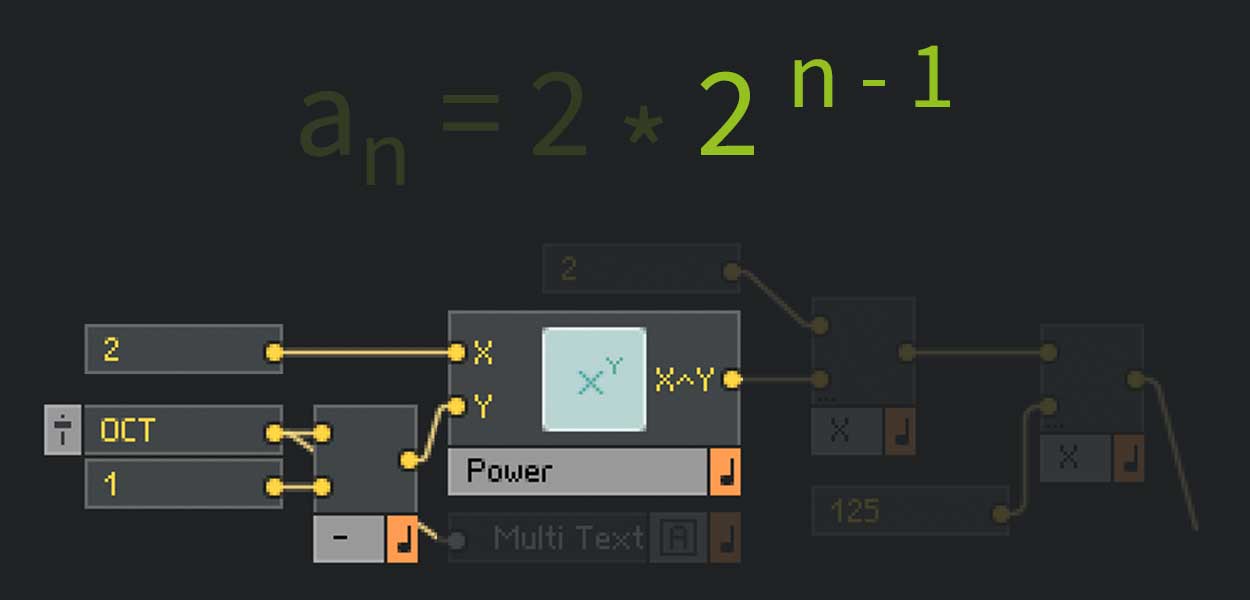
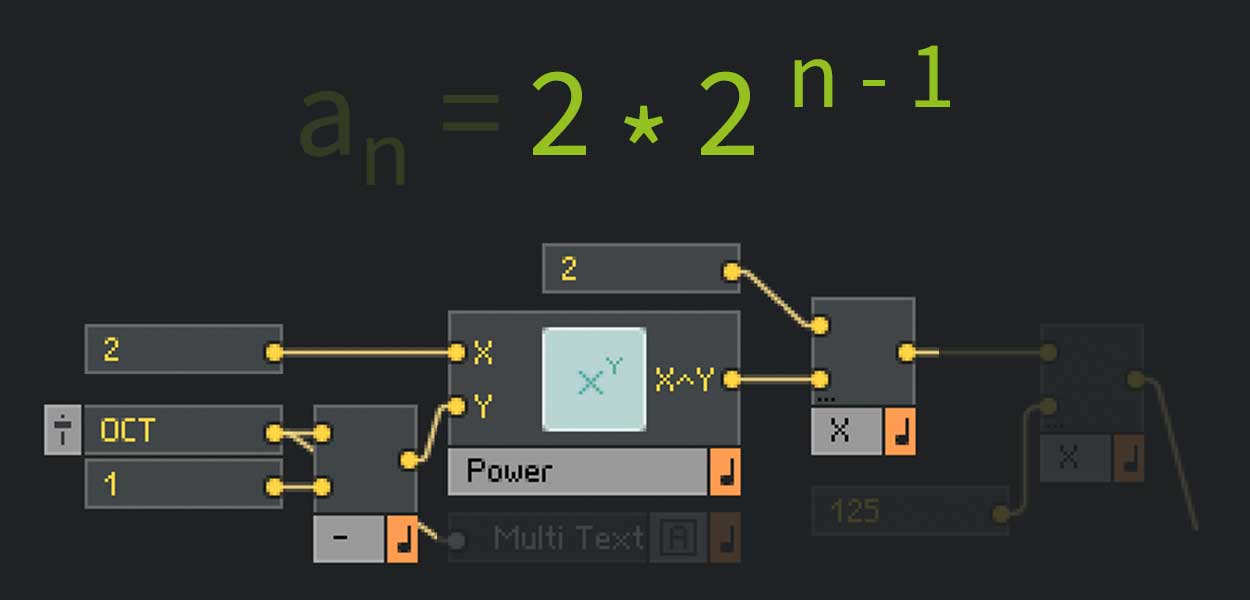
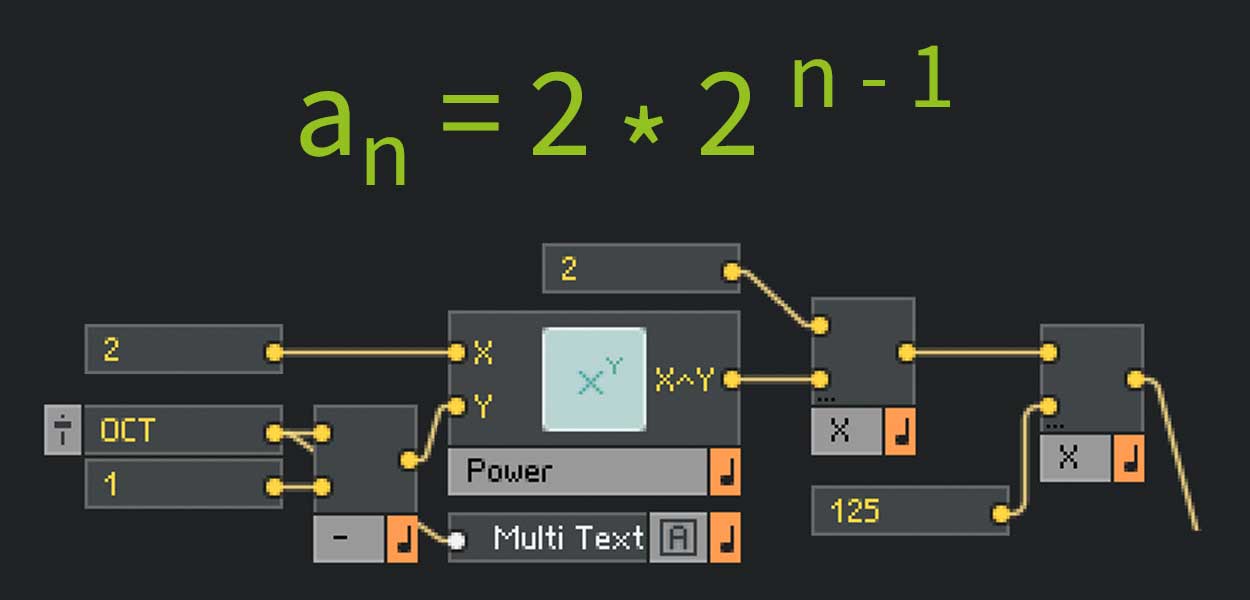
Abb. 12: Die Formel zur Oktavierungs-Logik
Der Einfachheit halber beginnen wir hinten: Der horizontale Fader mit der Bezeichnung „OCT“ und dem Wertebereich von 1 – 5 ist unsere Variable „n“. Von dieser soll der Wert 1 abgezogen werden. Das erreichen wir, in dem wir den Fader und eine Konstante 1 in in genau dieser Reihenfolge (oberer Eingang minus unterer Eingang) an ein Sub-Modul anschließen. Am Ausgang wird nun n-1 anliegen.
Abb. 13, Schritt 1/5
Der nächste Schritt ist die Potenz-Funktion. Eine Konstante 2 soll mit dem Ergebnis unserer letzten Rechnung (n-1) potenziert werden. Wir bemühen dazu das Power-Modul und schließen am X-Eingang die Konstante 2 und am Y-Eingang n-1 an, weil wir ja x^y rechnen wollen. Am Ausgang des Power-Moduls liegt jetzt 2^n-1 an.
Abb. 14, Schritt 2/5
Nun multiplizieren wir das Ergebnis mit 2, weil die Formel das so vorgibt. Dazu verbinden wir den einen Eingang des Multiplikators mit der Konstanten 2, den anderen mit dem bisherigen Ergebnis. Die Formel ist damit fertig.
Am Ausgang der Schaltung liegen nun – je nach Faderstellung – die Werte 2, 4, 8, 16 und 32 an. Nur noch ein letzter Schritt und wir erhalten die benötigte Zielfolge.
Abb. 15, Schritt 3/5
Jetzt gilt es noch die Konstante zu finden, die jeweils mit 2, 4, 8, 16 und 32 multipliziert die Werte 250, 500, 1000, 2000 und 4000 ergibt. Korrekt, es ist die 125. Also noch schnell das Ergebnis unserer Berechnungen und die Konstante 125 mit einem Multiplikator verbinden und das Ganze dort anschließen, wo sich bisher die Konstante 1000 befand. Fertig. Fast.
Abb. 16, Schritt 4/5
Da wäre dann noch das Multitext-Modul, das direkt an den Fader angeschlossen wird. Der Fader zeigt bestenfalls die Ziffern 1 – 5 an. Ein Multitext-Modul kann die Werte des Faders in frei festlegbare Ausgaben umleiten. Im Function-Reiter des Multi-Textes müssen also nur die Positionen 1 – 5 mit Inhalt belegt werden. (Der Multitext beginnt bei 0 zu zählen, weshalb die Position 0 leer gelassen wird). In diesem Fall habe ich die Positionen 1 – 5 nicht mit den Zahlen für die Oktavlage befüllt (also -2, -1, 0, +1, +2), sondern mit Skalen, bestehend aus senkrechten und waagerechten Strichen:
- – – – – I
- – – – I –
- – – I – –
- – I – – –
- I – – – –
Mit der Schrift Seminold und der Schriftgröße 13, lässt sich die Skala über dem Fader mit der Länge von 41 Pixeln genau so positionieren, dass die senkrechte Linie dem Fader folgt.
Eines noch: Da der größte Wert (4000) für die tiefste Lage steht und diese am Linken Ende des Faders liegen soll, ist hier Min: 5 und Max: 1. Nur falls ihr euch beim Studium der Teileliste gefragt habt. Und das erklärt auch, warum die Multi-Text Einträge mit dem Marker rechts beginnen.
Abb. 17, Schritt 5/5
Abb. 18: GUI – Serviervorschlag
Die oktavierte Saite
Einmal, von oben nach unten, durch die 5 Oktavelagen.
[06]
Bevor wir den ersten Teil verlassen …
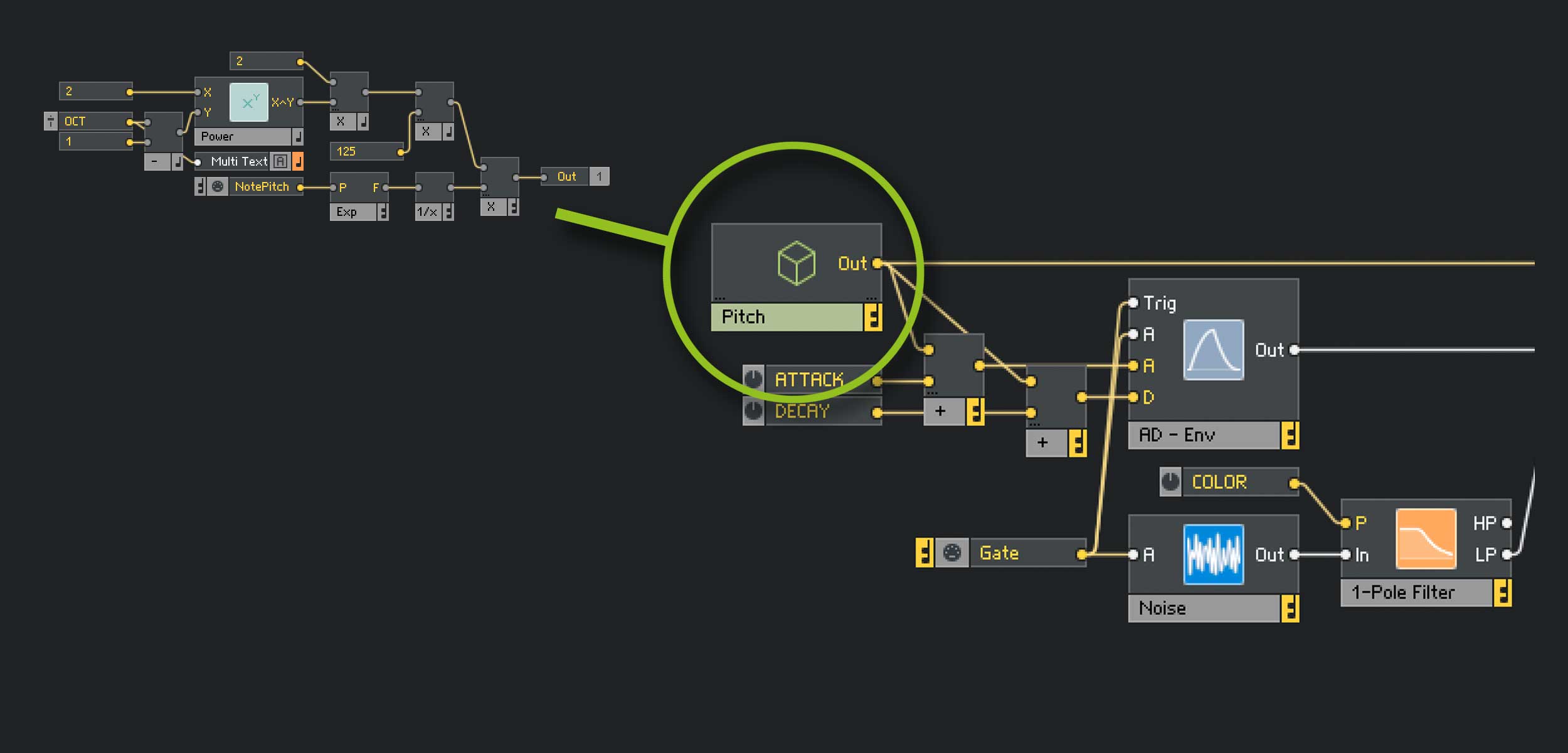
räumen wir noch ein wenig auf: Die mittlerweile recht komplexe Tonhöhensteuerung wird ein Macro verpackt:
Abb. 19: Die komplette Pitch-Schaltung im Macro
Kontakt
Bernd Scheurer
Mainstraße 2
64390 Erzhausen
Fon: 06150 865902
Mobil: 0151 50411034
unterricht@bernd-scheurer.de
Follow Me ...
Freie Plätze
- Erzhausen
- MO: 14:00 – 16:30 [anfragen]
- Langen
- DO: 13:30 - 14:00 [anfragen]
Infos
- Aktuelle Gebührenordnungen
Auch interessant
Newsticker
amazona
tastenwelt
klassik heute